标签:丁小平、教育、数学、微积分
义务教育应该有双重含义——开办者出于义务而开办,学习者尽自己的义务而学习。人类社会的进步虽然也是波浪式前进的,但是毕竟进入了开办义务教育的时代。如果一国政府不真正开办义务教育,哪怕是出于愚民政策的初衷,都是愚蠢的,因为,人类已经进入国民不读书就必然成为社会的拖累的时代。
教育事业的发展,尤其是进入义务教育时代以来,多数人产生了一种误解,以为学习就是教师在讲台上讲学生在台下听的过程,并且这样的学习是自然而然的,而自学则往往是一种无奈,不这样就是学习条件不达标,其实不然。真正的教育学家毛泽东指出:“学习就其本质而言是自学。”真是一语道破天机。

理论学习就是解决对事物的知其然和知其所以然的过程,而技能学习不过是在前者基础之上融入操作的过程而已。所谓知其然就是弄清楚一个事物是什么样子的;知其所以然就是弄清楚这个事物为什么是这个样子的。比如,公式法求解一元二次方程:
首先,知道
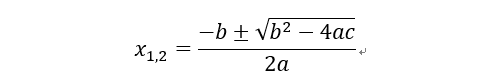
,并且,它是针对一元二次方程ax²+bx+c=0
而言的,x1,x2指的是这个方程的两个根,
a,b,c分别是方程二次项系数、一次项系数和常数项。这就是弄清楚一元二次方程求根公式是什么样子的过程,也就是说,只要是形如ax²+bx+c=0
的一元二次方程,我们把a,b,c
带入公式就可以得到方程的两个根。这个过程就是知其然。
其次,弄清楚

是怎么来的。
对于x²+x-6=0
,我们可以用配方法求解,即x²+x+(1/2)²=6+(1/2)²,
整理后,(x+(1/2))²=25/4
,然后,两端开方,得x+1/2=5/2或x+1/2=-5/2
,最后,x1=-3,x2=2。
同理,我们可以把a,b,c看作具体数字,采用配方法解ax²+bx+c=0:
第一步,把ax²+bx+c=0
写成配方法的规范形式,即x²+(b/a)x+(c/a)=0;
第二步,配方,即x²+(b/a)x+(b/2a)²=-(c/a)+(b/2a)²
,亦即(x+(b/2a))²=(b²-4ac)/4a²
,两端开方,然后,移项合并同类项,得

。
如上就是
的得来过程,这就是为什么一切形如ax²+bx+c=0
的一元二次方程的根为什么都是
。这就是所谓的所以然。
仅仅知道知其然和知其所以然还不够,还要知道谁知其然和谁知其所以然,当然,这个“谁”就是“我”,是“我”在学习。既然是“我”在学习,那么知其然和知其所以然的就得是“我”。因此,不管是自己独自完成这个过程还是他人讲给我这个过程,总之,都得“我”知其然和知其所以然。由此可知,自己独自完成这个过程还是他人讲给我这个过程都不过是手段,问题的根本在于知其然和知其所以然的得是“我”。即使他人向我讲解了一个事物是什么样子和为什么是这个样子,只要“我”没听或者没弄明白,最后,都没有意义,所以说,学习就其本质而言是自学。
古往今来,成大器者无不是自学或者以自学为主。依赖老师的学法不是最佳的。当然,这不是说老师可有可无,只是说那种持久战似的填鸭教育是得不偿失的。老师存在的意义往往在于,在学生不懂的、同时也非本课程内容但却与所学内容密切相关的知识方面给学生以指导。比如,制定学生学习战略和策略、指导怎样做人、交给学生学习方法、组织学生讨论等。还有就是解答学生弄不懂的问题、批改作业和试卷等。
没有老师是一种遗憾,可是,老师不一定是想有就有的。比如,老师来不了自然就没有老师,一个人要学的东西别人不会也不会有老师。对于没有老师的情况,一个人不自学或者自己研究又能怎么办呢?可见,自学是学习的根本。
当然,以上所说的自学讲的都是自遣意识中的自学,非自遣意识中的自学又有许多不同。生命动力、情感能力、审美能力、创新能力、感悟能力、想象能力和形象思维能力等等的提高都是非自遣教育和学习的内容,这方面的学习通过自学完成往往是异常困难的。比方说,医生可以给患者看病,医生也可以给自己看病,但是,对医学一窍不通的人给自己看病就困难了。非自遣性质的学习大多如此。
非自遣性质的自学不是不可以,而是其进展相对于老师指导要慢很多。非自遣性质的自学就好比一个水平不佳的医生给自己看病,在看病中提高医术;在提高医术后再看病,如此往复,不断提高。
理论的东西往往是纯而又纯的,理论上讲的自学和听课也是如此。而现实中纯而又纯的事物是不存在的,因此,纯自学也是不存在的。自学者也要在该请教的时候就请教。















