很多时候,数学题目中的关键解题信息就像高卧隆中的隐士一样,躲在各种各样的信息后面深藏功与名,,需要你反复求索才能把他们请出山林。

我们来看看下面图1这道题:
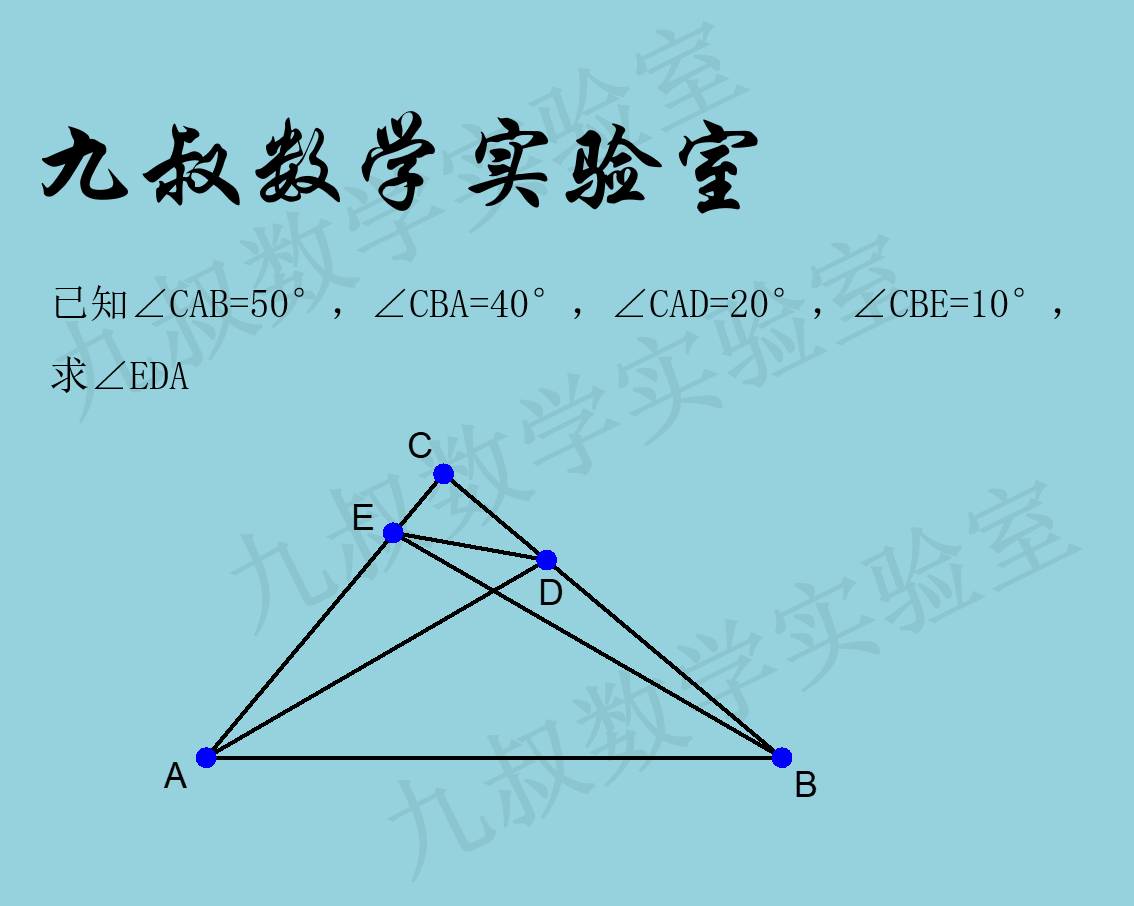
图1
数学题有一个规律:通常内容很简洁,寥寥数语就完事的题目都是闷骚型的,能让人脑袋抽筋的狠角色。

这道题完全没有长度信息,也没可用的特殊形状信息,只有角度信息,但是如果你想通过各个子图形的角度关系来推算出目标角的角度的话,最后你会发现自己陷入在一个死循环里绕来绕去,就是绕不出目标角的角度。
过去老一辈国家建设者常说的一句话,叫“有条件要上,没有条件创造条件也要上”。这道题也是这样,没有特殊形状信息,我们可以给它创造。下面我们就按图2添加辅助线来创造特殊图形:
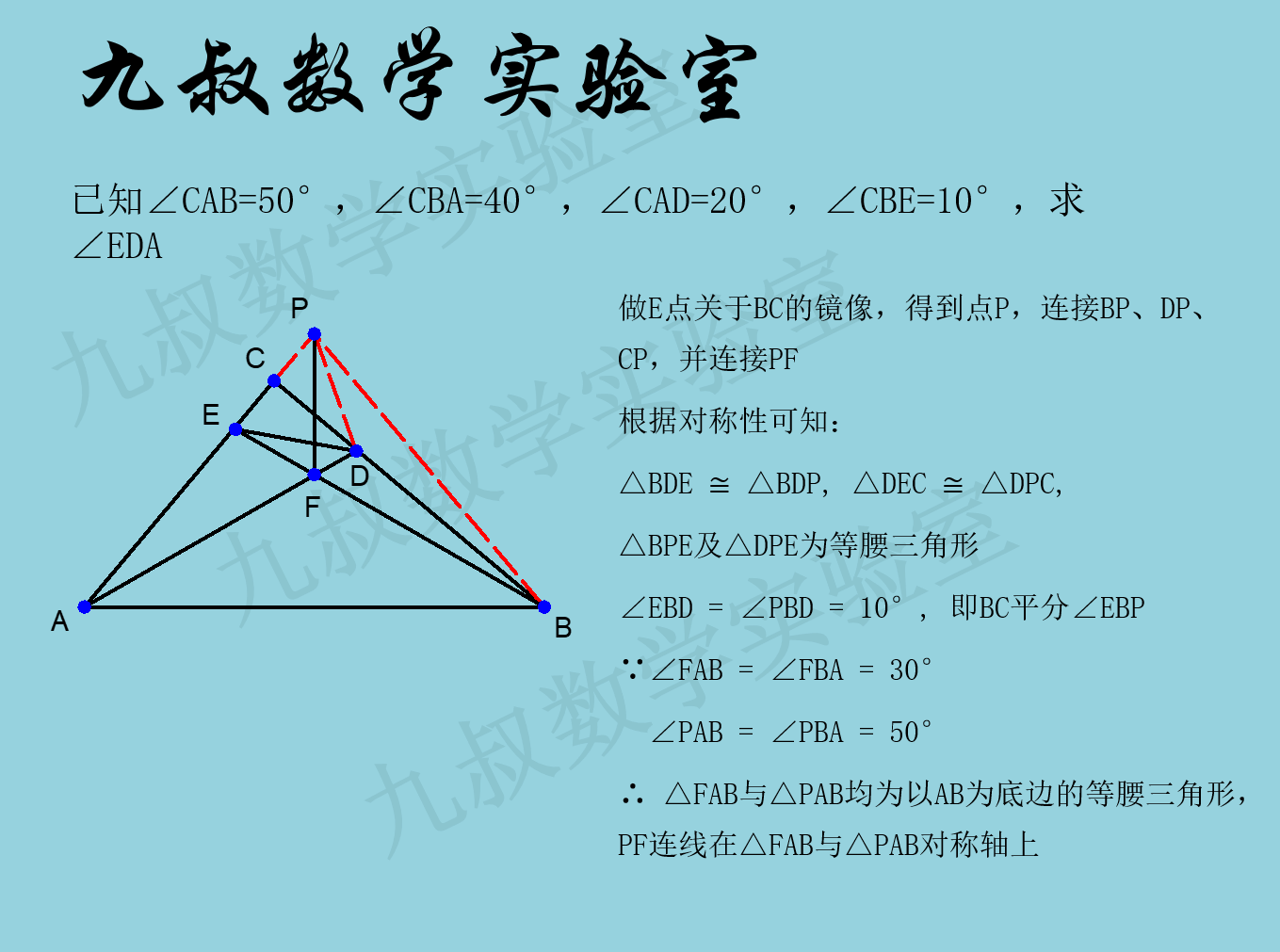
图2
通过创建图2中所示的辅助线,我们创造了几对全等三角形:△BDE与△BDP,△DEC与△DPC,△BEC与△BPC;同时也创建了几个等腰三角形:△BPE、△DPE、△PAB及△FAB.。接下来,爱思考的你不妨先自己思考一下看能否算出目标角度,再考虑是否要读后面的答案。

思考时间,先提高一下学霸修养
在添加辅助线后,不仅要看到辅助线所构造的几组全等图形和几个等腰三角形,还需要看到BD、FD构成了△BDP的内心,从而挖掘出本题解题的关键信息:PD平分C,进而挖掘出△PED为等边三角形这一关键信息,最终计算出∠EDA。
图3是具体的求解过程,请各位参考:
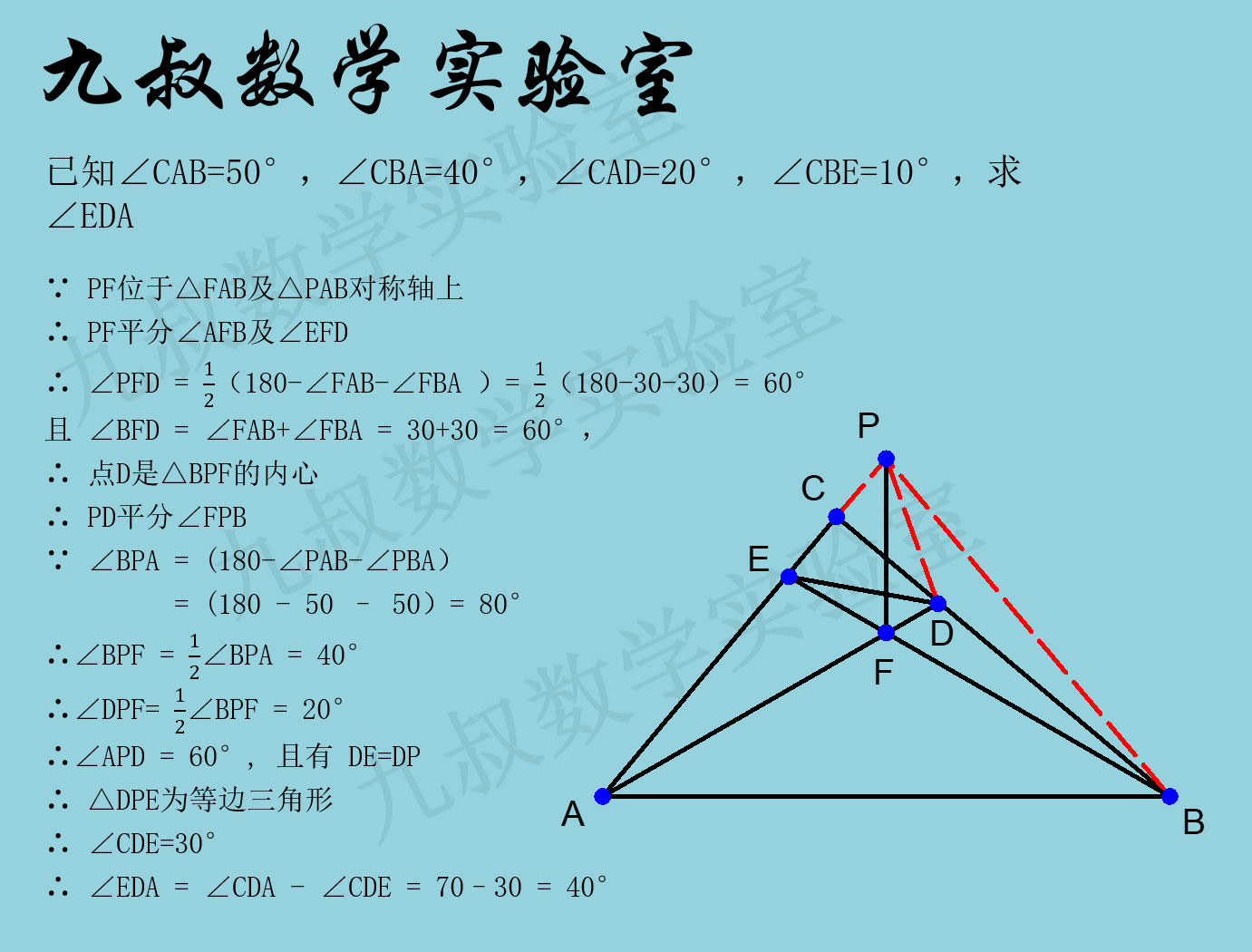
图3
相信很多人都想到了构造E点的镜像点P,但是大多数人由于没有发掘出FD平分∠PFB的信息,自然也不会想到PD平分∠BPF,就更无从进一步求解了。
这道题确实有一定难度,但应该还有其他解算方法。如果你想到了不同的解算方法,欢迎多指教哦。














